Solution to The Spider and the Fly Problem

The answer is 40 feet.

Figure A below shows the "obvious" but wrong solution where the distance that the spider travels (d) is 42 feet.

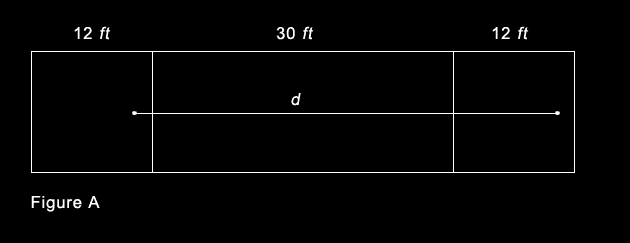
Figure B below shows an alternative route. The distance (d) can be calculated using the Pythagorean Theorem. The distance (d) is the hypotenuse of a right angle tirangle with the other sides measuring 37 and 17 feet. Therefore d = √(37² + 17²) = √(1658) which is apporximately equal to 40.7 feet.

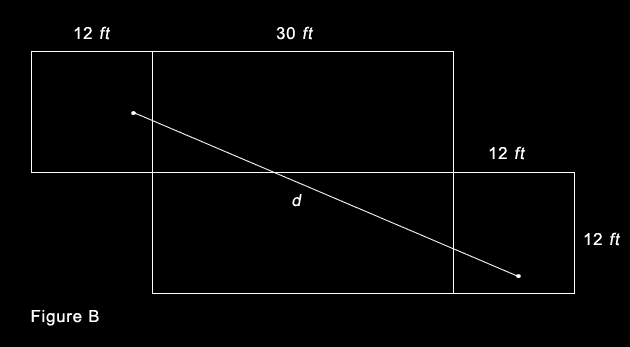
Figure C below shows the shortest possible route that the spider can take. Again the distance (d) can be calculated using the Pythagorean Theorem. This time the other two sides measure 32 and 24 feet.
Therefore d = √(32² + 24²) = √(1600) = 40 feet.

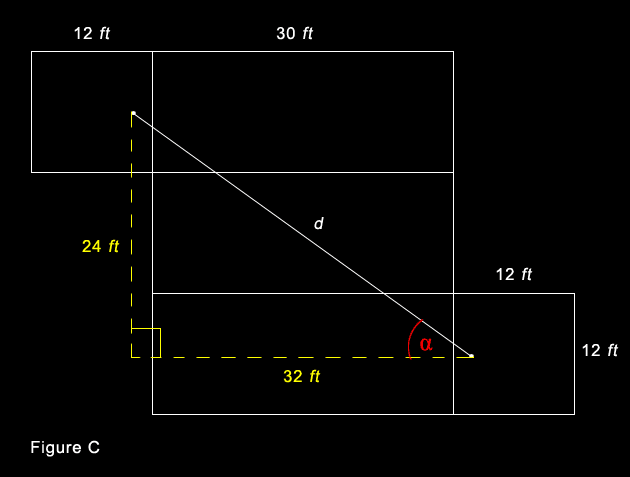
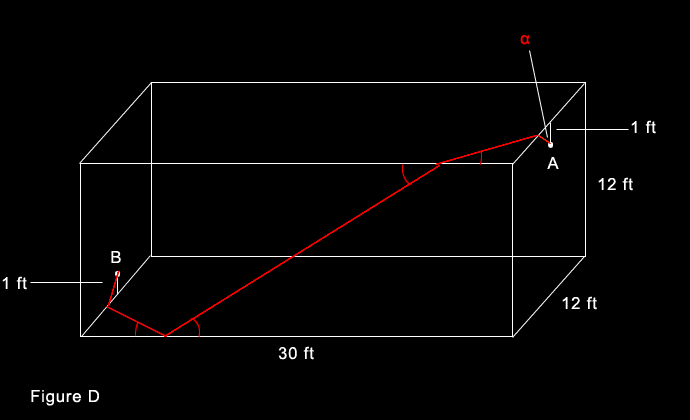
The angle α in figure C (above) is the angle at which the spider must set off in order to take to shortest route to the fly. In figure D (below) this is the angle between the red path taken by the spider and the perpendicular to the nearest edge (the short vertical line from A to the nearest edge).

This angle can be calculated using simple trigonometry: Tan α = O/A = 24/32 = 3/4 = 0.75. Therefore α ~ 36.87 degrees.

With a little imagination you should also be able to see how this angle can be used to determine the shortest route for the rest of the spider's journey.

ADDENDUM

In discussion of this puzzle in his book, The Pythagorean Thoerem, Eli Maor observes: "The entire route takes the spider through five of the six faces of the room; it demonstrates that the 'direct' route [figure A] is not always the shortest possible route – the geodesic – for that particular surface under consideration."

This is analogous to the problem of finding the shortest distance between two places on Earth which share the same latitude such as Edinburgh in Scotland and Moscow in Russia (both 55 degrees North). The shortest route between these two cities is NOT along the line of latitude. This becomes more apparent when one considers two points marked on a small cirlcle drawn around the North Pole (with the North Pole as the circle's origin). Clearly, the shortest route between these two points is not to walk around the circumference of the circle (the line of latitude) but to cut across a segment of the circle.

In general, the shortest route between two points of the same latitude lies on th arc of a great-circle whose centre is the centre of the Earth. Thus, the only time when the shortest route between two places of the same latitude is along their shared line of latitude is when the two places lie on the equator (a great-circle whose centre is the centre of the Earth).

If a straight line is defined as the shortest distance between two points, it can be seen that, apart from the equator, Earth's lines of latitude are not straight. Indeed, it can also be seen that straight lines drawn on the Earth (such are the equator) cannot be infinite but are limited to a maximum distance equal to the circumference of the Earth. This is one example of why Euclidean geometry does not work on the curved 2 dimensional surface of a 3 dimension sphere.

Similarly, the Pythagorean Theorem does not hold true on the curved surface of a sphere. Although it would work as a good approximation when drawing a very small right-angle triangle on a very large sphere, the theorem becomes increasingly inaccurate as the size of the triangle increases. Imagine drawing a giant triangle with one of its sides drawn along a quater of the length of the equator. At one end of this line, draw a line perpendicular (90 degrees) to the equator all the way to the North Pole. At the North Pole draw another line at 90 degrees and extend it to the equator. This line will also meet the equator at 90 degrees. Thus all three angles of this right-angle triangle are 90 degrees (summing 270 degrees) and sides are all of equal length.

This concept of a 2 dimensional suface being curved in 3 dimensional space producing non-euclidean geometry is often used as an introduction to Einstein's Thoery of Relativity which requires one to conceive of 3 dimension space being curved in four dimensions.

Confused? If you are interested to understand more about Einstein's Theory of Relativity, curiouser.co.uk recommends "Simply Einstein: Relativity Demystified" by Richard Wolfson; an excellent introduction to the subject for the lay reader.