Solution to the Monty Hall Problem

Mr Whitaker’s question soon became known asThe Mony Hall Problem (or the Monty Hall Paradox), named after the host of a popular American TV game show called “Let’s Make a Deal”, in which contestants were given a similar choice.

In response to her answer, Ms. Savant received an estimated 10,000 letters, many from learned academics, the vast majority of which told her she was wrong in no uncertain terms (see appendices).

A subsequent front page article of The New York Times in read: “Her answer... has been debated in the halls of the C.I.A. and the barracks of fighter pilots in the Persian Gulf. It has been analyzed by mathematicians at M.I.T. and computer programmers at Los Alamos National Laboratory in New Mexico. It has been tested in classes ranging from second grade to graduate level at more than 1,000 schools across the country.”

The surprising truth is that the Ms. Savant was correct.

If one assumes that the host deliberately opens a door which he knows will reveal a goat, you DOUBLE your chances of winning by switching to the other door.

Interestingly, if the host didn’t know where the car was and just opened a door at random to reveal a goat, switching doors would make no difference; the probability of either of the remaining doors revealing the goat in this instance would be ½.

(Unfortunately, the way the question was originally asked was slightly ambiguous, but we shall proceed as though it were stated that the host not only knew where the car was but deliberately opened a door that would reveal a goat. If, despite his knowledge, the host had used a random process for selecting which door to open, the probability of winning the car would not be changed if the contestant switched doors.)

Many people believe that it makes no difference whether or not you change doors in the problem as it was originally stated. They believe that the chances of either of the remaining doors revealing a car is ½. They are WRONG.

Click HERE to launch an excellent computer simulation of the Monty Hall Game, written and kindly donated to curiouser.co.uk by Stefan Knutsson.

The Explanation

There are various ways that this counter-intuitive answer can be explained:

1) Consider this: in what cases will switching doors lead to a goat? If one chooses a goat door originally, then switching doors can only lead to a car, as there is only one other goat door and that has been opened. Therefore, the other door must reveal the car. Conversely, if one selects the car door originally, switching doors must lead a goat.

One can therefore see that the only time when switching doors can be wrong is when one selects the car door originally. If one selects a goat door originally, switching must lead to the car. The probability of selecting the car door originally is 1/3. The probability of selecting a goat door originally is 2/3. Therefore the probability of winning the car by changing doors is 2/3. And the probability of losing the car by changing doors is 1/3. Therefore, the rational decision, as Ms. Savant stated, is to change doors in order to double the probability of winning the car.

2) Considering the following diagram:

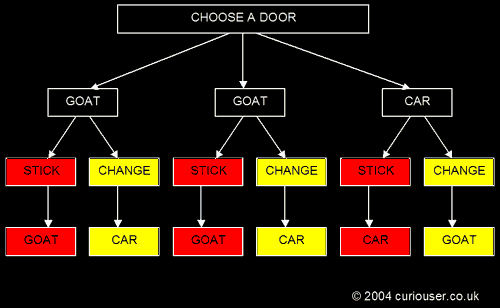
This diagram clearly shows that if you change your selection, 2 times out of 3 you will the car. If you don’t change your selection, you will only win the car 1 time in 3. You are therefore twice as likely to win if you change your selection.

3) Although not a proof, many people have only been convinced by the verity of Ms. Savant’s answer after conducting their own experiments and seeing the results for themselves.

A simple way to conduct a similar experiment is with 3 playing cards:

Select 3 aces, 1 red and 2 black. Shuffle the cards and lay them face down, so that you know where the red ace is. Ask someone to try to guess where the red ace is. After he/she has made his/her choice, turn over an unselected black ace and ask your friend is he/she wants to change his/her selection. Repeat the experiment as many times as possible with as many people as you like. Keep a log of how the success or failure rate for choosing the red ace depending on whether the original selection is changed or not. You will observe, as you conduct more trials, that the percentage of times when changing selection leads to a red ace will tend towards 66.7% and the number of times when not changing selection leads to a red ace will tend towards 33.3%.

It is important to note that the act of turning over a card that is known to be a black ace does NOT change the probability of having selected the red ace in the first place. However, were one of the non-selected cards to be turned over by someone who did not know whether it was back or red, and it turned out to be black, the probability of the selected card being red would then increase from 1/3 to ½ and it would make no difference whether or not the selected card was changed. Clearly, in this instance, if the turned card was a red ace, the probability of either of the remaining cards being red would diminish to 0. [See "Aha Gotcha", Ref. 1.]

4) If all else fails, try some mathematics:

Let the 3 doors be A, B and C.

Let your selection be A.

Let the door the host reveal be B.

The a priori probability that the prize is behind door X = P(X) = 1/3

The probability that Monty Hall opens door B if the prize were behind A is:
P(Monty opens B|A) = 1/2

The probability that Monty Hall opens door B if the prize were behind B is:
P(Monty opens B|B) = 0

The probability that Monty Hall opens door B if the prize were behind C is:
P(Monty opens B|C) = 1

Therefore:

The probability that Monty Hall opens door B is:
p(Monty opens B) = p(A) * p(Monty opens B|A) + p(B) * p(Monty opens B|B) + p(C) * p(Monty opens B|C) = 1/6 + 0 + 1/3 = 1/2

Using Bayes's Theorem:

P(A|Monty opens B)	= p(A) * p(Monty opens B|A)/p(Monty opens B)
	= (1/6)/(1/2)
	= 1/3

and

P(C|Monty opens B)	= p(C) * p(Monty opens B|C)/p(Monty opens B)
	= (1/3)/(1/2)
	= 2/3

In other words, if you choose A originally and Monty opens door B to reveal a goat, the probability of there being a car behind door C is 2/3. Therefore you should always switch your selection

5) Finally, it is worth considering what would happen it there were more than 3 doors. Let us assume there are 10 doors, with 9 goats and 1 car. The contestant selects one door. The host, Monty Hall decides to open 8 doors that he knows will all reveal goats. What is the probability now of winning the car if the contestant decides to change his/her selection? Again, there is only one way in which changing the selected door can lead to a goat, and that is if the contestant selected the car door originally. If the contestant didn’t select the car door originally, then the other door must reveal the car. The chances of the contestant selecting the car door originally are just 1/10. Therefore the probability of winning the car by changing selection in this instance is 9/10.

In general, with n doors, and (n-2) goat doors knowingly opened by the host, the probability of winning the car by changing from the original selection is (n-1)/n.

For a more in depth discussion of what happens when more complex permutations of doors and choices are introduced, see "A three-door game show and some of its variants", Ref. 7.

Appendices

Here is a selection of comments received by Ms. Savant in repsonse to the answer she gave in her column:

"As a professional mathematician, I'm very concerned with the general public's lack of mathematical skills. Please help by confessing your error and, in the future, being more careful."
Robert Sachs
(Professor of mathematics , George Mason University, Fairfax, Va)

"After removing my foot from my mouth I'm now eating humble pie. I vowed as penance to answer all the people who wrote to castigate me. It's been an intense professional embarrassment."
Robert Sachs (again)

“You are utterly incorrect…How many irate mathematicians are needed to get you to change your mind?”
E. Ray Bobo, Ph.D., Georgetown University

“If all those Ph.D.s were wrong, the country would be in very serious trouble.”
Everett Harmann, Ph.d., U.S. Army Research Institute

References

1. Martin Gardner, aha! Gotcha. Paradoxes to puzzle and delight, Freeman & Co, NY, 1982

2. J. de Pillis, 777 Mathematical Conversation Starters, MAA, 2002, pp. 143-146

3. Marylin vos Savant, The Power of Logical Thinking, St. Martin's Press, NY 1996 .

4. S.K.Stein, Strength in Numbers, John Wiley & Sons, 1996 .

5. Mark Haddon, The Curious Incident of the Dog in the Night-time, Vintage, 2003.

6. John Tierney "Behind Monty Hall's Doors: Puzzle, Debate and Answer?", The New York Times July 21, 1991, Sunday, Section 1; Part 1; Page 1; Column 5

7. Bapeswara Rao, V. V. and Rao, M. Bhaskara: "A three-door game show and some of its variants", The Mathematical Scientist 17 (1992), no. 2, pages 89-94