US President J.A. Garfield's proof of the Pythagorean Theorem

The following proof of the Pythagorean Theorem was discovered in by President J.A Garfield in 1876.

The Pythagorean Theorem states that for any right triangle of sides a, b and c, where c is the hypotenuse, c² = a² + b²

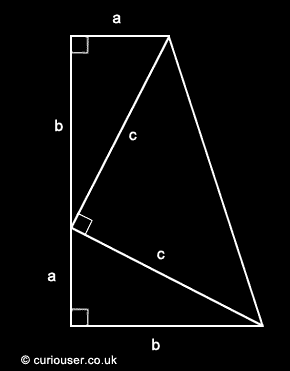
The formula for the area of a trapezoid is: half the sum of the bases times the height.

Therefore, the area of the trapezoid in the diagram above can be calculated as:
(a + b)/2 · (a + b)

However, the area can also be calculated as the sum of the three triangles:
ab/2 + ab/2 + c · c/2

Therefore:
(a + b)/2 · (a + b) = ab/2 + ab/2 + c · c/2

which simplifies to:
(a + b)² = 2ab + c²

Thus:
a² + b² + 2ab - 2ab = c²

so:
c² = a² + b²

Q.E.D.